Isolation by Resistance Sampling
Landscape genetics has laddered null hypothesis regarding the genetic structure of species. The first null, Panmixia, is that populations show no differentiation, as could be observed in a species with few, highly connected populations; it is not treated as a sampling scenario by this package. The second null is Isolation by Distance, the main idea behind most of the functions in this package, where populations become more differentiated as a function of geographic distance - culminating in the function ‘IBDBasedSample’. The final null hypothesis is Isolation by Resistance, where the differentiation of populations is driven by environmental distances across populations decreasing gene flow.
While IBD is easily calculated from geographic distances, IBR
requires a parameterized cost surface, in raster format, that depicts
the costs to an organism’s movement of maternal and paternal genetic
material. safeHavens supports a simple workflow to
paramterize a cost surface, that can be used to support basic
IBR type sampling.
Example
We’ll use the species occurrence data from dismo again here. A few
spatial data sets that should be suitable for nearly all users IBR
applications are included in safeHavens for this example,
but the full data sets are not shipped with the package. They include: -
lakes, Lehner et al. 2025, GLWD
- oceans from Natural Earth, https://www.naturalearthdata.com/downloads/10m-physical-vectors/
- rivers from FAO,
- tri (terrain ruggedness index), Amatulli et al. 2018, https://www.earthenv.org/topography
We’ll load the species occurrence data and make it explicitly spatial.
data prep
Each of the environmental variable data sources needs some pre-processing before being feed into the IBR workflow, most of them just need to be converted from vector to raster formats - a process we call ‘rasterization’. We will also rescale the tri rasters, to put them on a similar numeric range as the other data sets.
tri <- terra::rast(file.path(system.file(package = "safeHavens"), "extdata", "tri.tif"))
names(tri) <- 'tri'
rescale_rast <- function(r, new_min = 0, new_max = 1) {
r_min <- global(r, "min", na.rm = TRUE)[[1]]
r_max <- global(r, "max", na.rm = TRUE)[[1]]
((r - r_min) / (r_max - r_min)) * (new_max - new_min) + new_min
}
tri <- rescale_rast(tri, 0, 100)
lakes_v <- sf::st_read(
file.path(system.file(package = "safeHavens"), "extdata", "lakes.gpkg"),
quiet = T) |>
filter(TYPE == 'Lake') |> # remove reservoirs for our purposes (time scale)
select(geometry = geom) |>
mutate(Value = 1) |> # this will be rasterized.
terra::vect()
ocean_v <- sf::st_read(
file.path(system.file(package = "safeHavens"), "extdata", "oceans.gpkg"),
quiet = T) |>
select(geometry = geom) |>
mutate(Value = 1) |>
terra::vect()
rivers_v <- sf::st_read(
file.path(system.file(package = "safeHavens"), "extdata", "rivers.gpkg"),
quiet = T) |>
select(geometry = geom) |>
mutate(Value = 1) |>
terra::vect()We’ll convert each of the above spatVect objects to spatRasters, and clip them to an area of analysis around our species records.
x_buff <- sf::st_transform(x, planar_proj) |>
# huge buffer for the bbox.
st_buffer(200000) |>
st_transform(crs(lakes_v)) |>
st_as_sfc() |>
st_union() |>
vect() |>
ext()
lakes_v <- crop(lakes_v, x_buff)
rivers_v <- crop(rivers_v, x_buff)
ocean_v <- crop(ocean_v, x_buff)
tri <- crop(tri, x_buff)The vector data need to be converted to raster format using a
function like rasterize, from terra.
ocean_r <- rasterize(ocean_v, tri, field = 'Value', background = 0.1)
lakes_r <- rasterize(lakes_v, tri, field = 'Value', background = 0.1)
rivers_r <- rasterize(rivers_v, tri, field = 'Value', background = 0.1)
par(mfrow=c(2, 2))
plot(rivers_r)
plot(lakes_r)
plot(ocean_r)
plot(tri)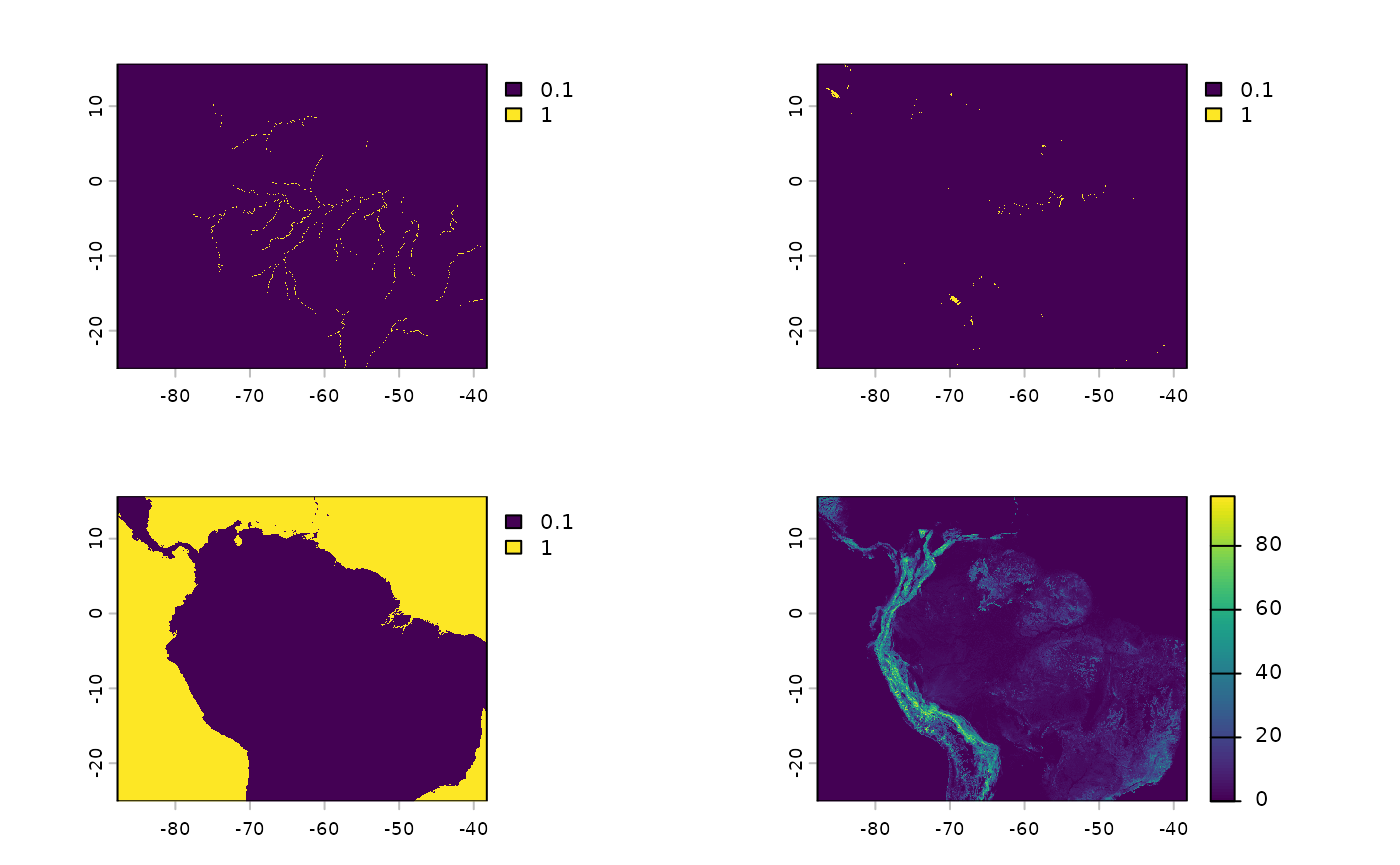
actual workflow.
The first, of three, functions in the Isolation by Resistance
sampling workflow is used to create the resistance surface. It requires
a template raster, and the other rasters which will be incorporated into
the product. buildResistanceSurface essentially just
requires the rasters we configured above, and user specified weights to
assign to each raster. These weights convey how difficult it is for a
species to move across the landscape. For plants, oceans generally get
very high weight, while lakes and rivers - still obstacles - receive
lower weights. Terrain ruggedness values are much more likely to vary
based on both the ecology of the species, and the lanscape being
sampled.
When considering weights consider the influences of: bird dispersal, land animal dispersal, and natural growth/expansion of populations. This is certainly the most difficult part of this workstream to tune, and often relies on subjective expert judgement. The values below are the functions defaults - to my eyes they work OK for the landscape at hand; although an ecologist with experience in this region may beg to differ, and I would not argue with them.
res_surface <- buildResistanceSurface(
base_raster = rast(ocean_r), # template
oceans = ocean_r, # rasters
lakes = lakes_r,
rivers = rivers_r,
tri = tri,
w_ocean = 120, # weights to multiple input raster values by --
w_lakes = 50, # is 1 * 50
w_rivers = 20, # is 1 *20
w_tri = 4 # ranges from 1~30, so from (1-30)*4 up to a weight of ~120.
)
plot(res_surface)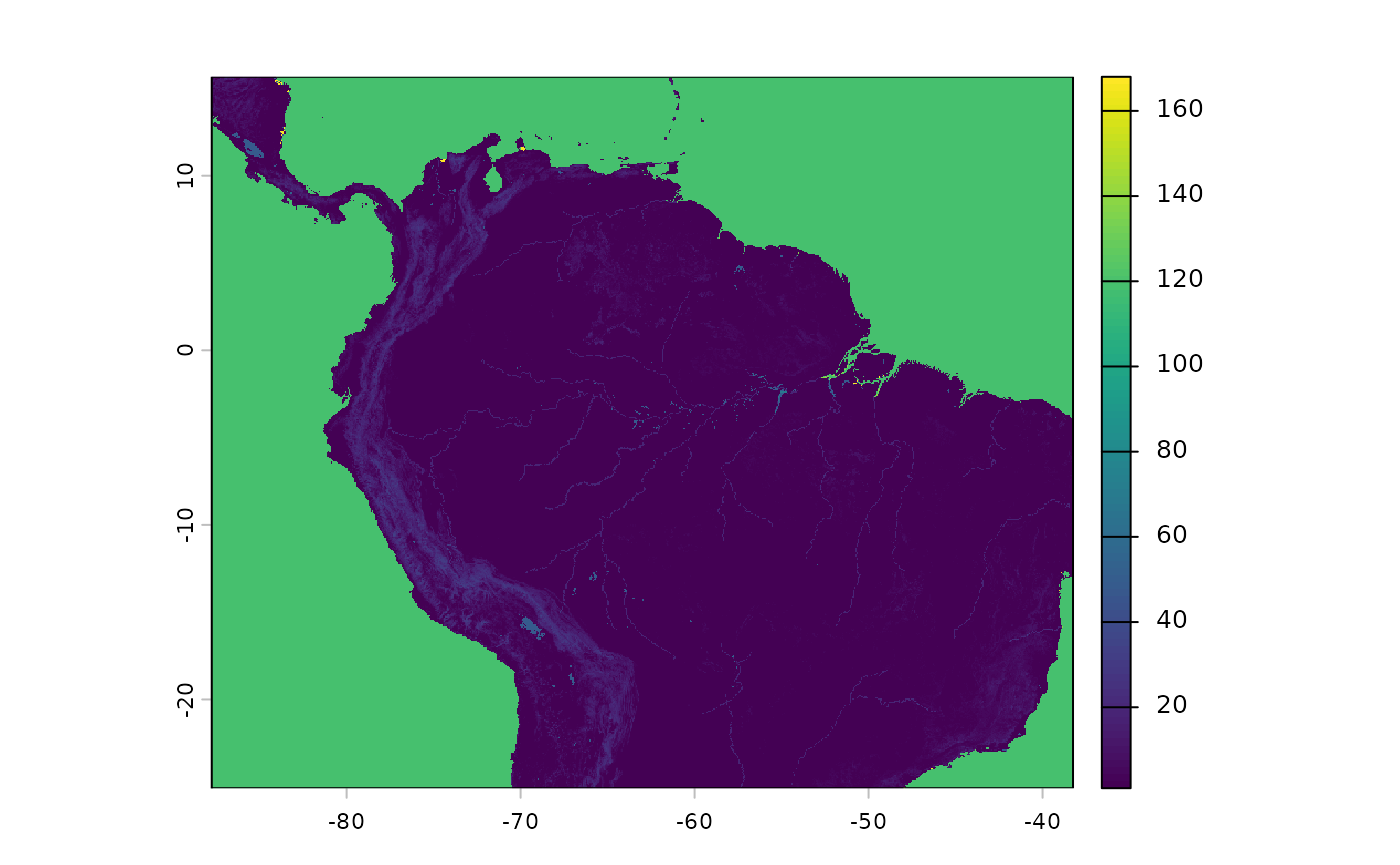
Note that the above object will be stored in memory, I advocate for the use of a relatively coarsely grained raster surface (e.g. 4kmx4km cells or more), because we are doing pretty generalized work, and it will speed up processing.
Now that we have our resistance surface, the next step is calculating
the distances between areas across the species range. Similar to other
functions in safeHavens we will not use population
occurrence record data directly, as we know that spatial biases affect
occurrence record distributinons. Rather we will buffer
(buffer_dist) the occurrence records, using a relevant
planar_proj, and create a raster surface of their
locations. From this surface we will sample n points (using
terra::spatSample, with method = ‘spread’), and identify neighboring
points using a graph_method, either delauney triangulation,
which is useful when a very high n is required, or through
a complete distance matrix.
In my testing I greatly prefer results from ‘complete’
calculations, and these work with NbClust without having to be ordinated
down into 2-dimensional space and give much better results.
This function will return a raster representing the buffered populations (species range in the domain), the points sampled by terra, the graph information, and a distance matrix with the least cost distance values from the resistance surface.
pop_res_graphs <- populationResistance(
base_raster = rast(ocean_r),
populations_sf = x,
n = 150,
planar_proj = 3857,
buffer_dist = 125000,
resistance_surface = res_surface,
graph_method = 'complete'
)
names(pop_res_graphs)
#> [1] "pop_raster" "sampled_points" "spatial_graph" "edge_list"
#> [5] "ibr_matrix"The buffered locations look like this - currently the IDs are meaningless.
plot(pop_res_graphs$pop_raster)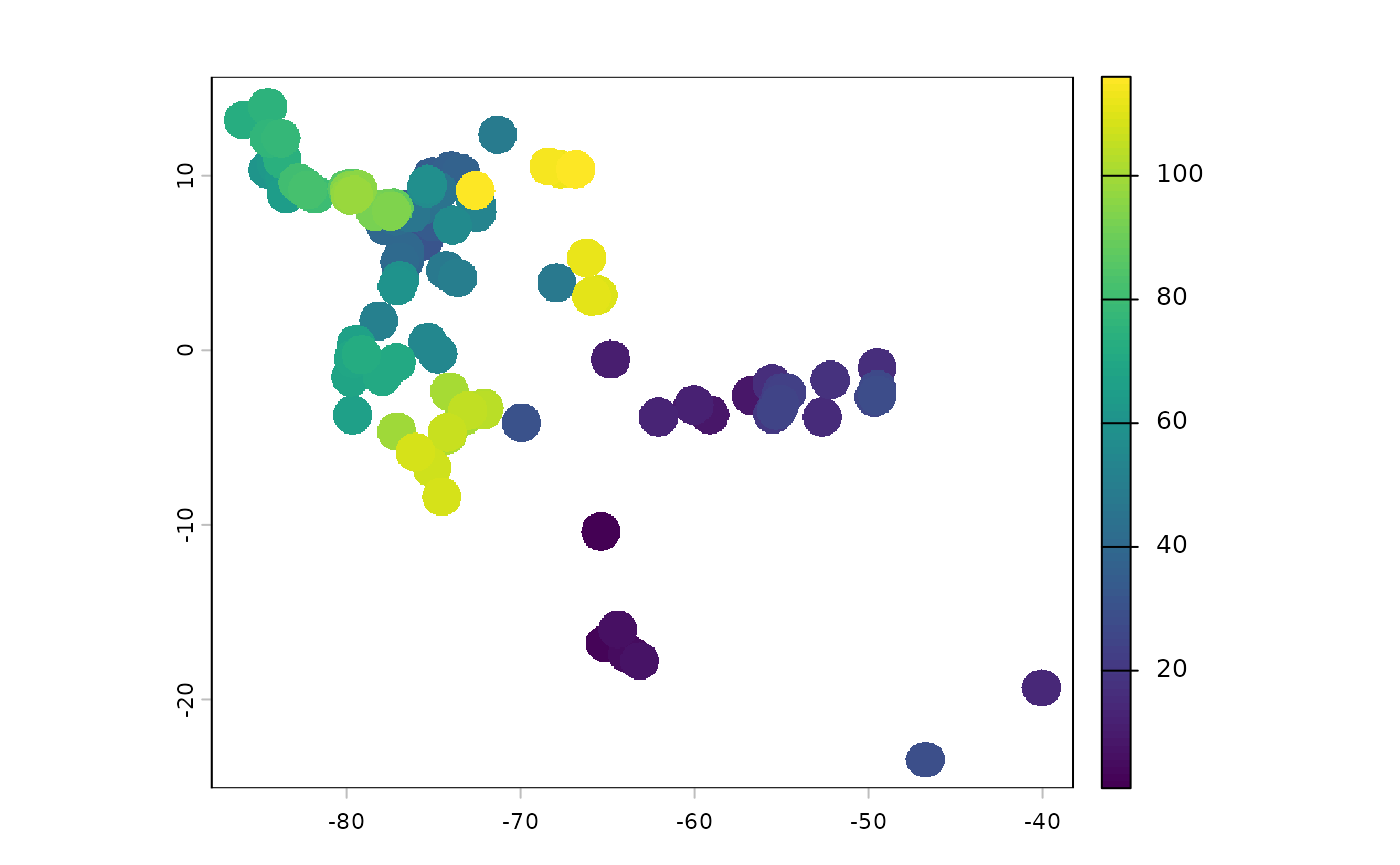
This function does not perform well with user pre-specified
n, however the min.nc parameter, passed to
NbClust can be applied to generally give the analyst
specified value.
ibr_groups <- IBRSurface(
base_raster = rast(ocean_r),
resistance_surface = res_surface,
pop_raster = pop_res_graphs$pop_raster,
pts_sf = pop_res_graphs$sampled_points,
ibr_matrix = pop_res_graphs$ibr_matrix,
fixedClusters = TRUE,
n = 20,
planar_proj = 3857
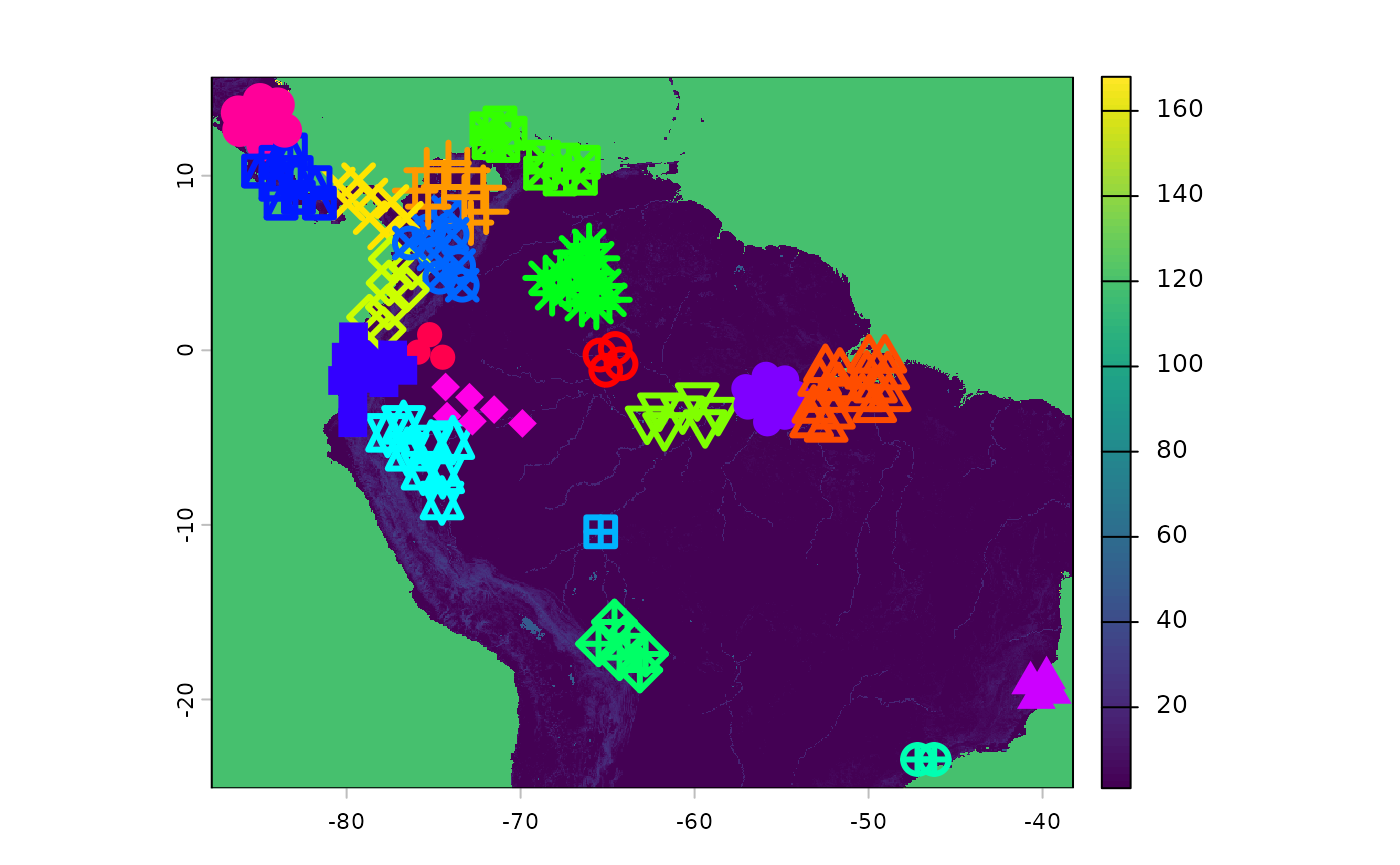
)The results of the clustering process are visualized beneath.
classified_pts = ibr_groups$points
plot(res_surface)
points(
classified_pts,
pch = as.numeric(as.factor(classified_pts$ID)), # different symbol per ID
col = rainbow(length(unique(classified_pts$ID)))[as.factor(classified_pts$ID)],
cex = 2,
lwd = 3
)
The classified occupied area clusters are visualized below.
ggplot() +
geom_sf(data = ibr_groups$geometry, aes(fill = factor(ID))) +
theme_minimal()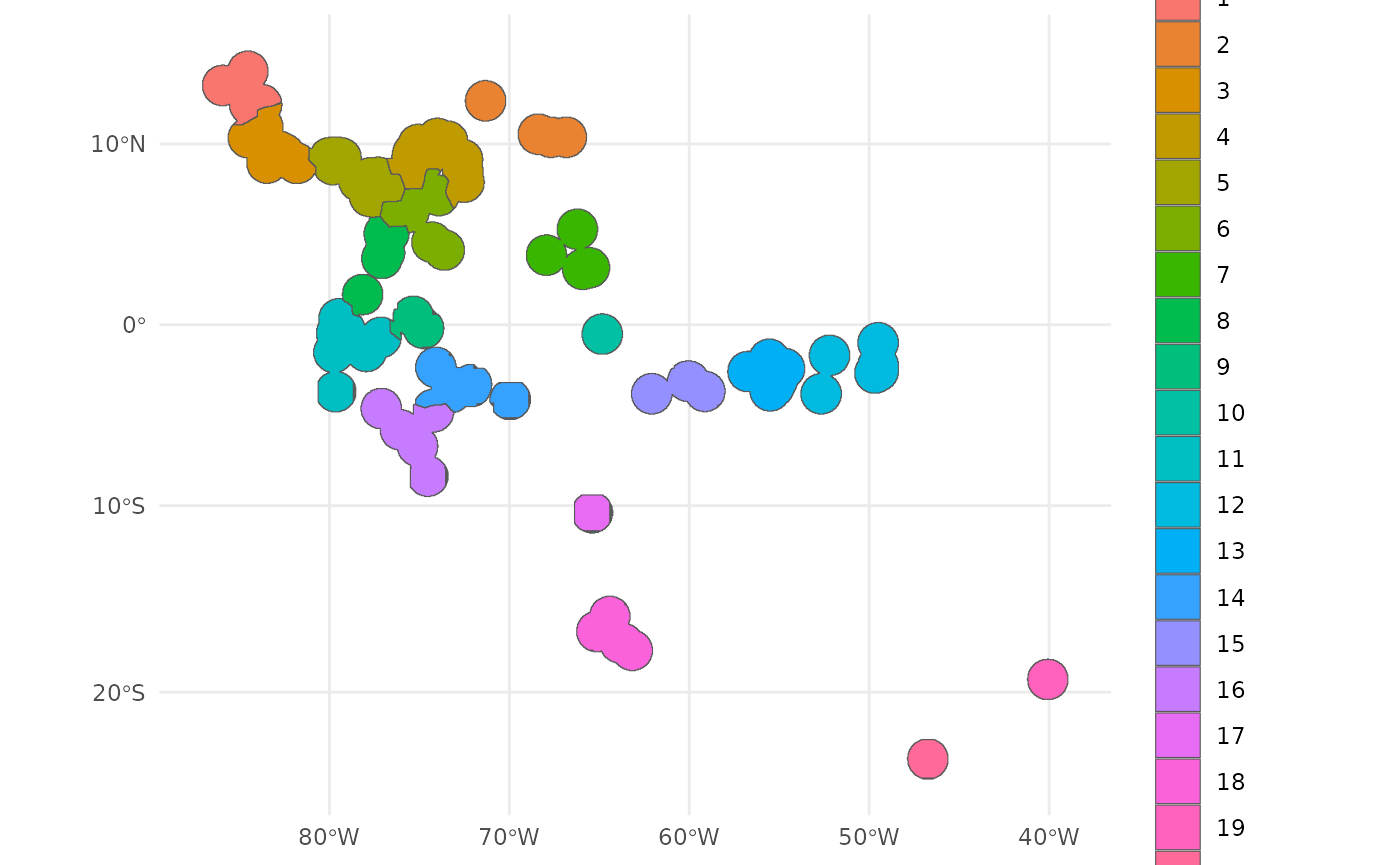
Finally the surface can be sampled using
PolygonBasedSample. Simply union the geometries to be the
species range, and supply the groups to the x argument, in lieu of an
ecoregion or pstz type surface.
out <- PolygonBasedSample(
x = st_union(ibr_groups$geometry),
zones = ibr_groups$geometry,
zone_key = 'ID',
n = 30
)
ggplot(data = out) +
geom_sf(aes(fill = factor(allocation))) +
theme_minimal() +
labs(fill = 'Ct. collections\nper cluster') +
theme(legend.position = 'bottom')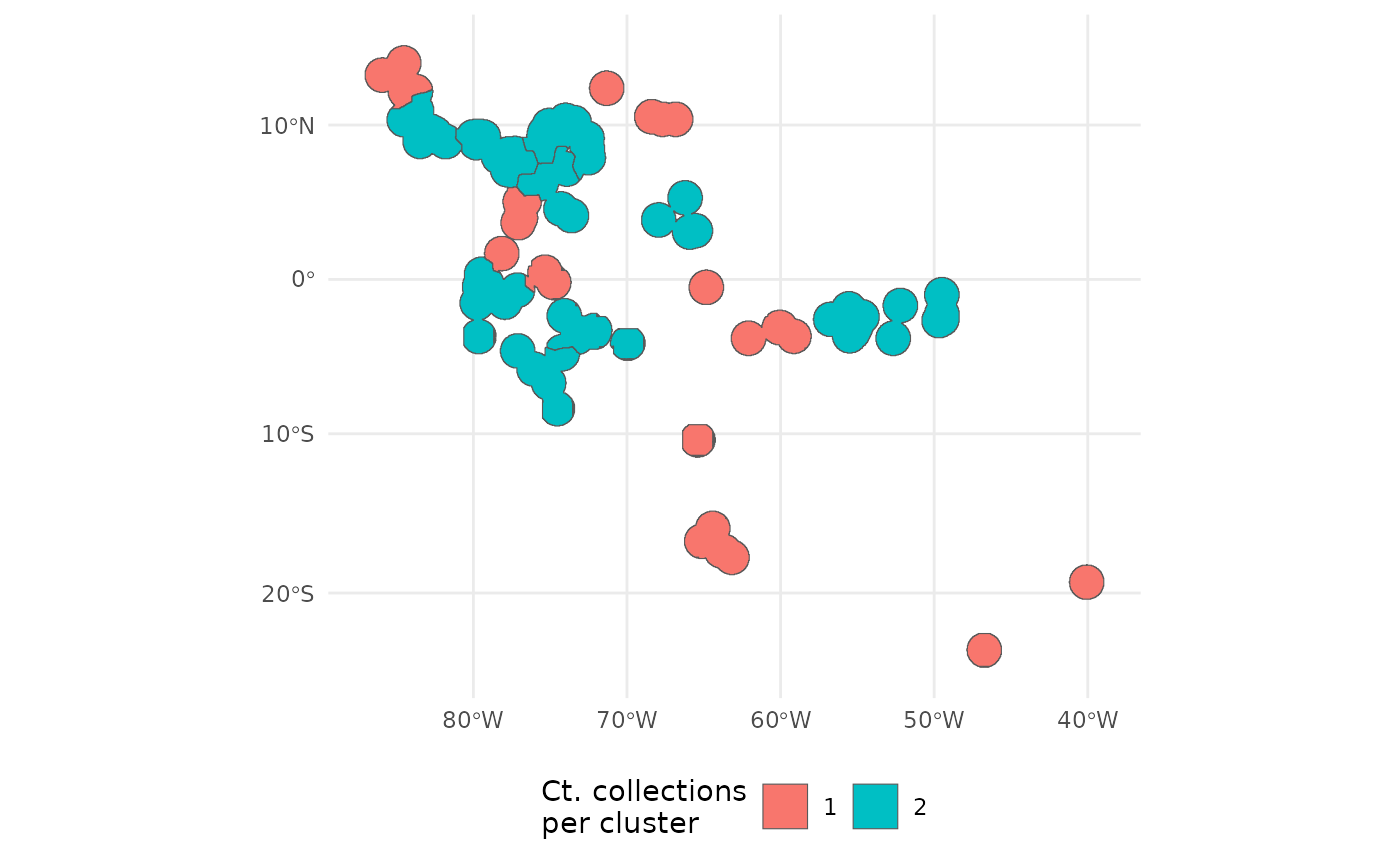
Each of the nine clusters has a different number of the 20 desired collections assigned to it.
bonus: adding sdm as a resistance layer, and non-linear scaling.
A default argument to cluster IBR is the probablity surface predictions from an SDM. Here we will add it to the surface.
We will also show another way of adding topographc ruggedness index, that ‘bypasses’ an assumed linear relationship along the weighting scheme.
sdm <- terra::rast(
file.path(system.file(package="safeHavens"), 'extdata', 'SDM_thresholds.tif')
)
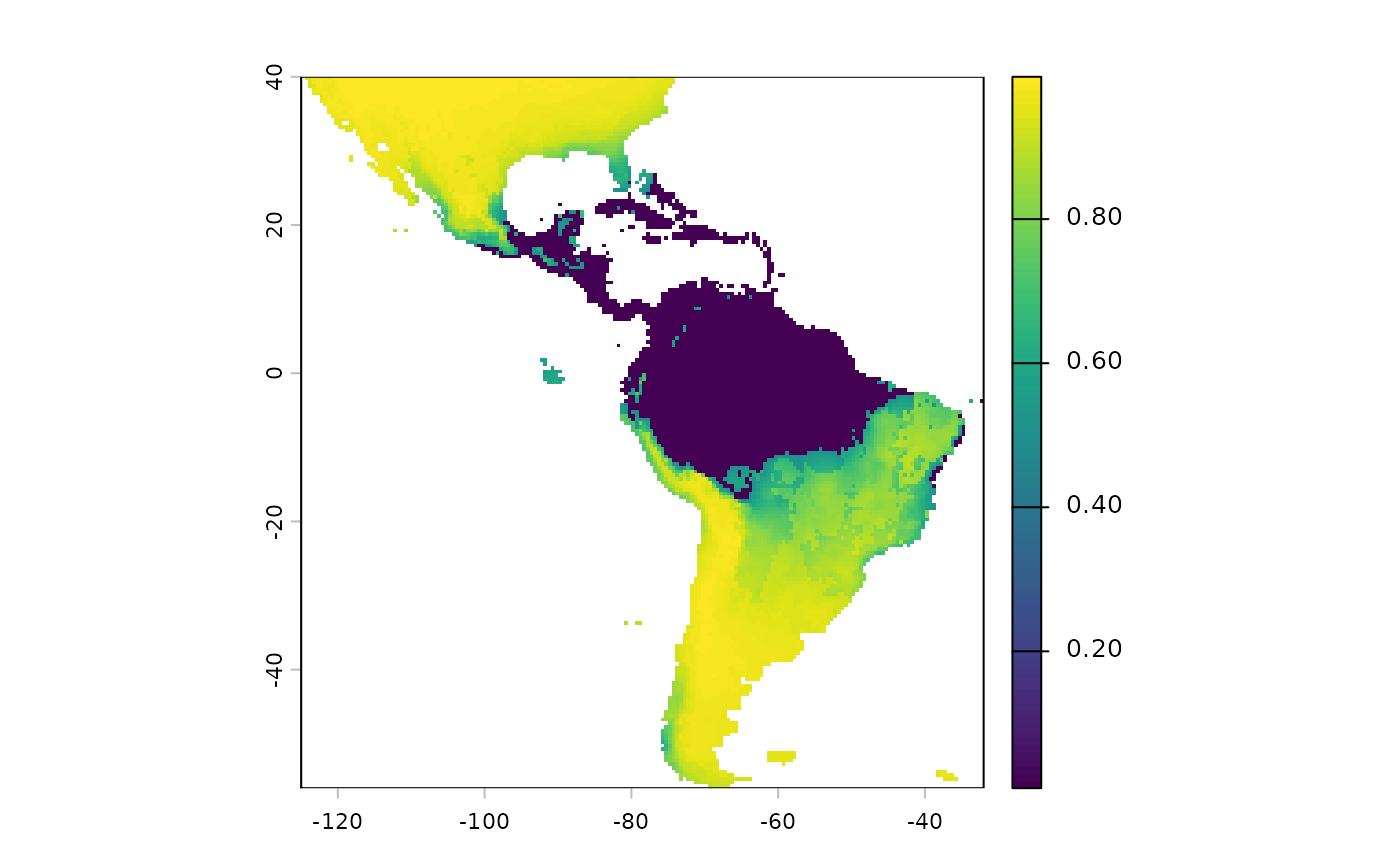
plot(sdm['Predictions'])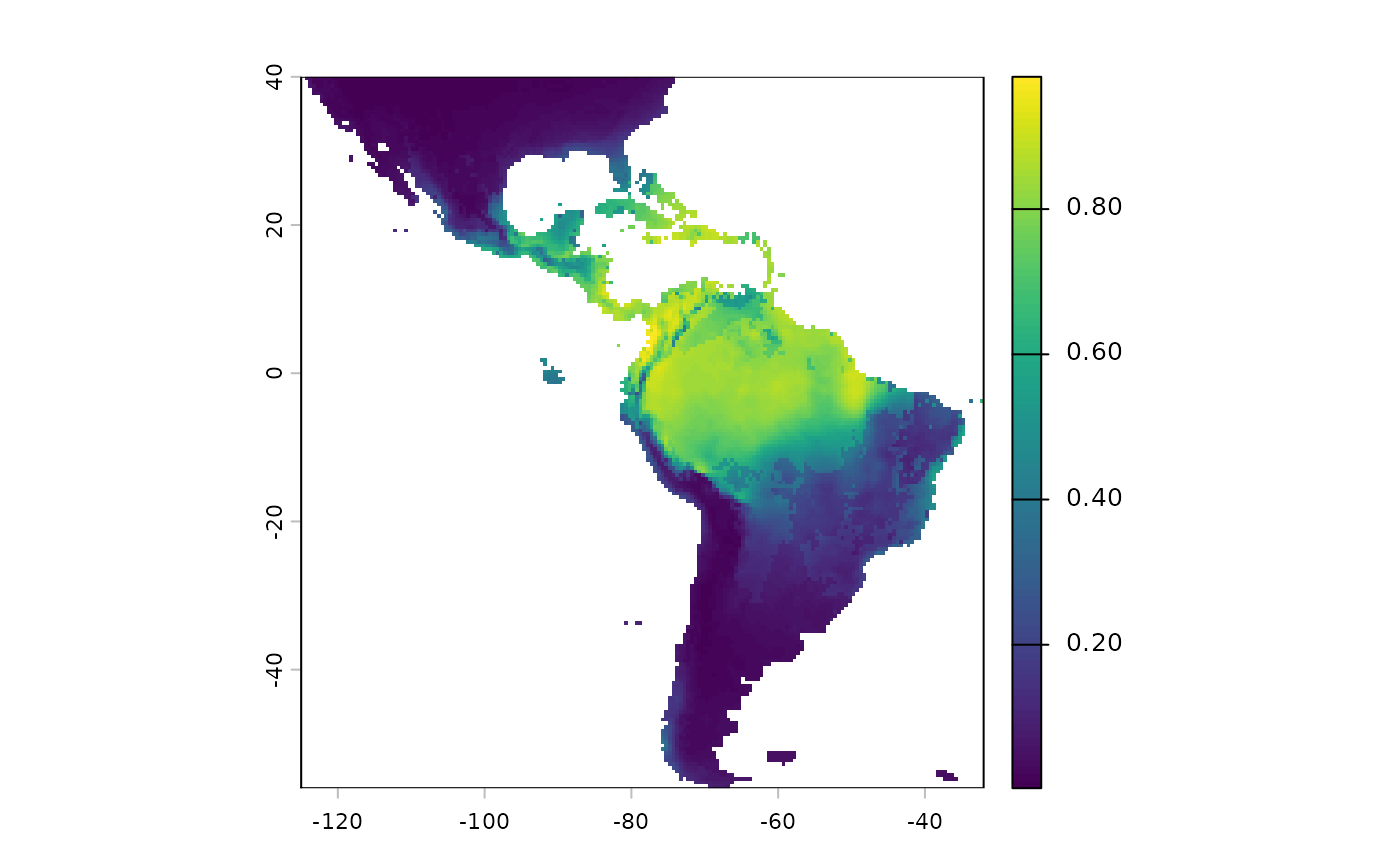
Note that we will have to reverse the predictions from this layer, currently higher values mean more suitable habitat. We want the higher values going into the probability surface function to mean more resistance to movement.
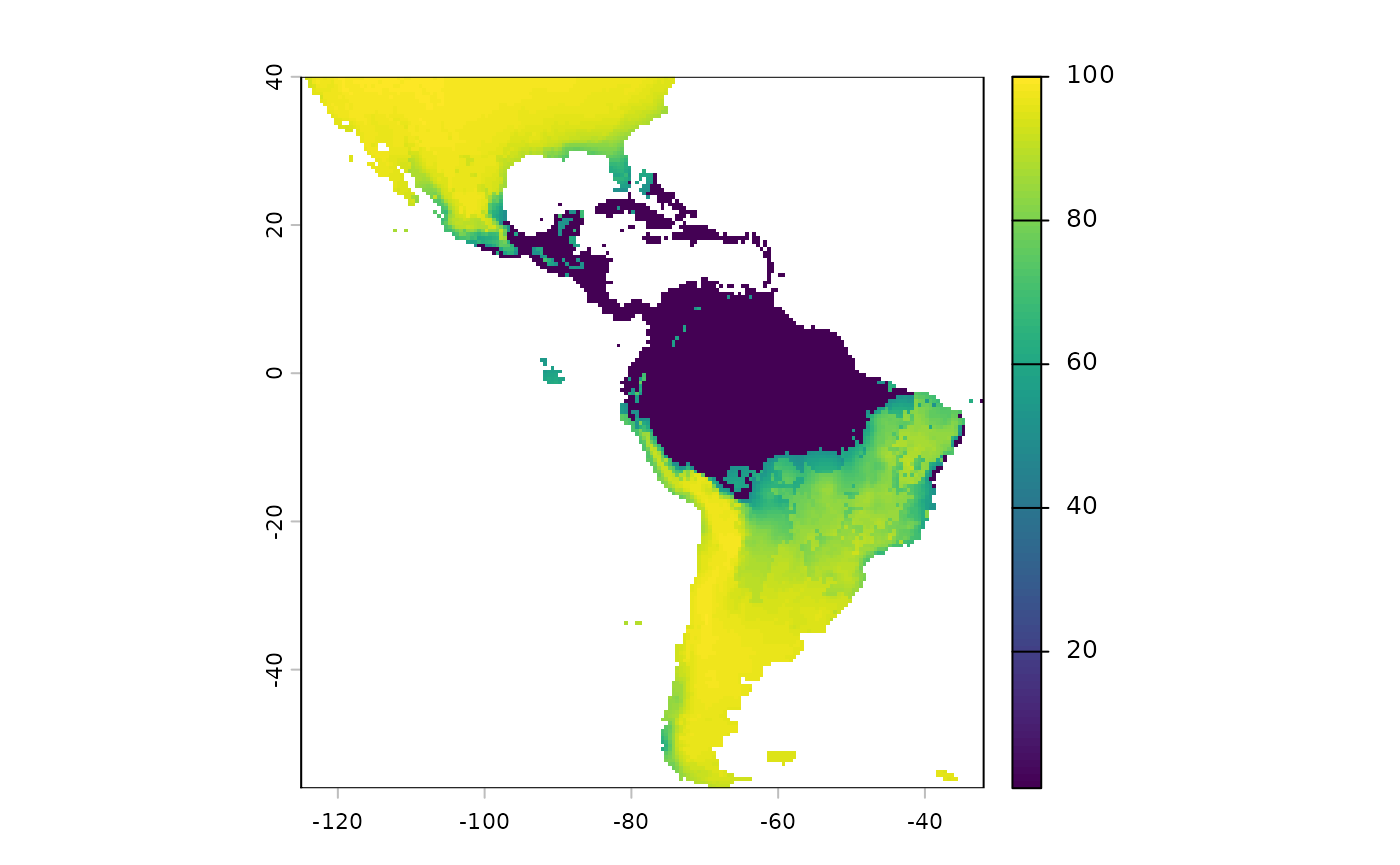
inverted_sdm <- 1 - sdm['Predictions']
plot(inverted_sdm)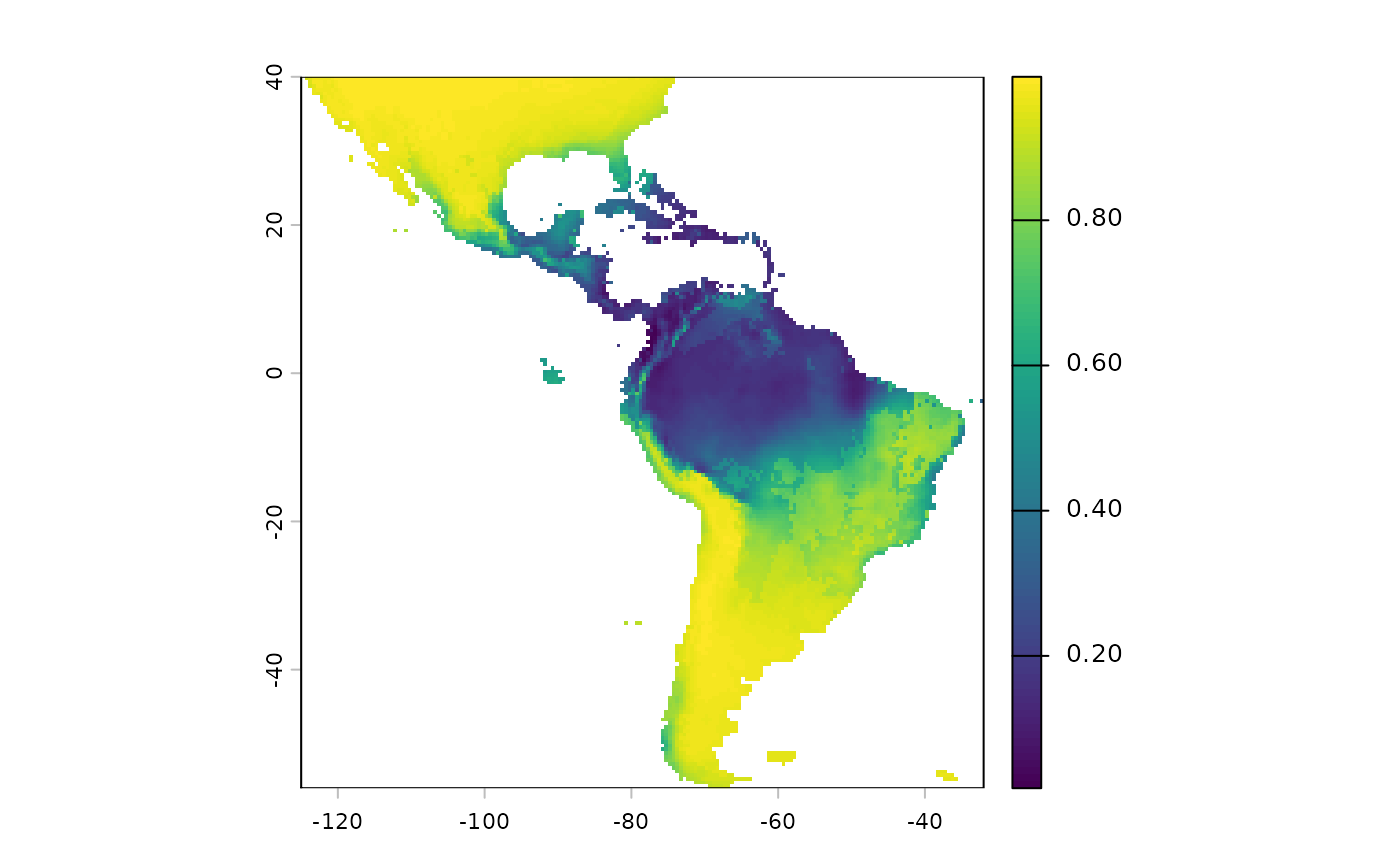
And indeed, we may actually just want to remove weights in suitable habitat, or set to an arbitrarily low value
And we will convert it to the same, integer, scale as the rest of the predictors
Note that we will have to make sure our SDM aligns with the existin layers
inverted_sdm <- crop(inverted_sdm, ocean_r)
inverted_sdm <- resample(inverted_sdm, ocean_r)
inverted_sdm[is.na(inverted_sdm)] <- 99
plot(inverted_sdm)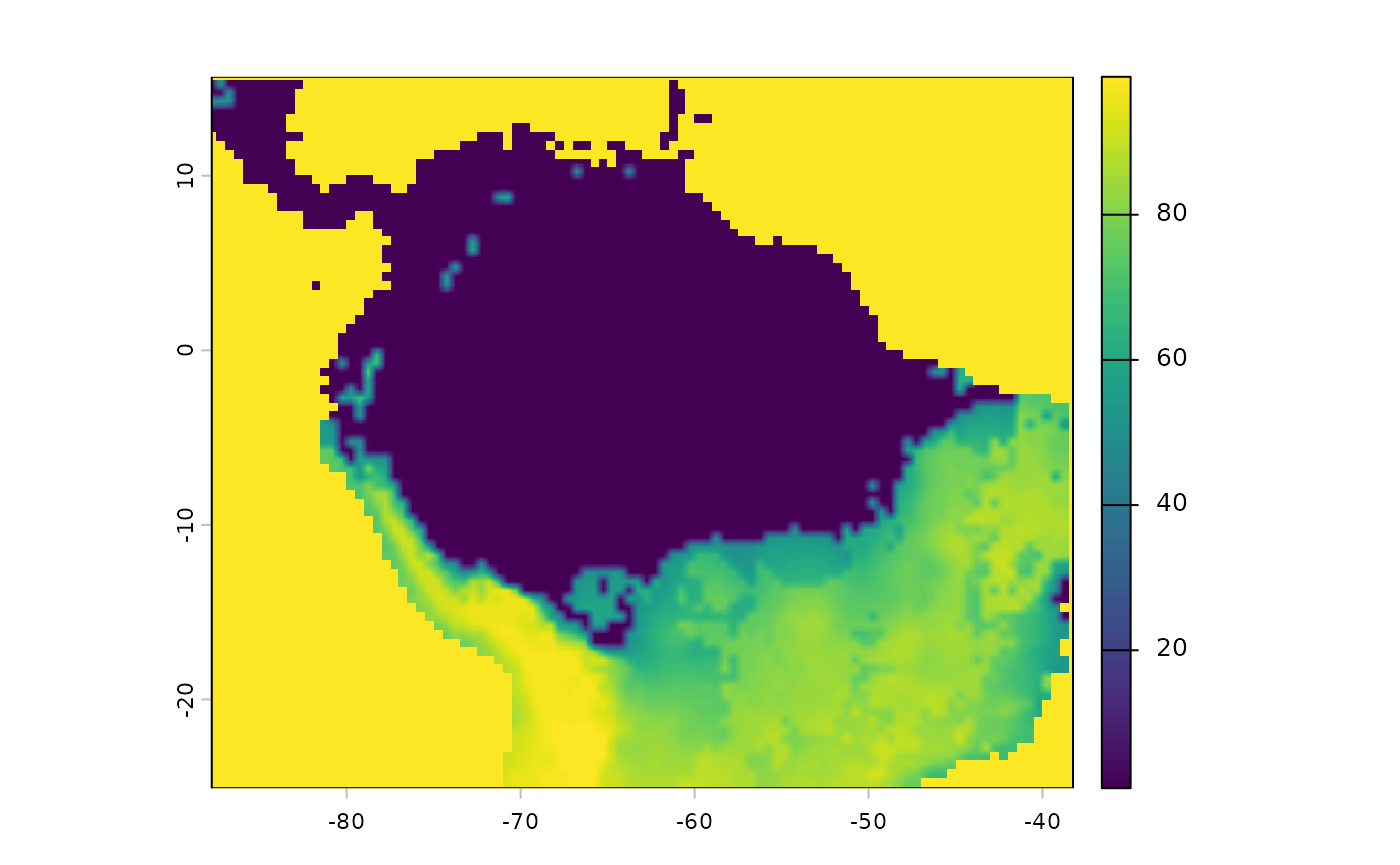
non-linear weight
Not all environmental variables are expected to have linear effects on movement. Indeed something like terrain ruggedness may have only a small effect until reaching certain thresholds.
x <- 1:100
rs <- function(x, to = c(0, 100)) {
rng <- range(x, na.rm = TRUE)
to[1] + (x - rng[1]) / diff(rng) * diff(to)
}
# display some transformations.
par(mfrow = c(2, 3), mar = c(4, 4, 2, 1))
plot(x, rs(sqrt(x)), type = "l", main = "sqrt(x)")
plot(x, rs(log1p(x)), type = "l", main = "log1p(x)")
plot(x, rs(asinh(x)), type = "l", main = "asinh(x)")
plot(x, rs(x^2), type = "l", main = "x^2: polynomial")
plot(x, rs(x^3), type = "l", main = "x^3: polynomial")
plot(x, rs(x^4), type = "l", main = "x^4 polynomial")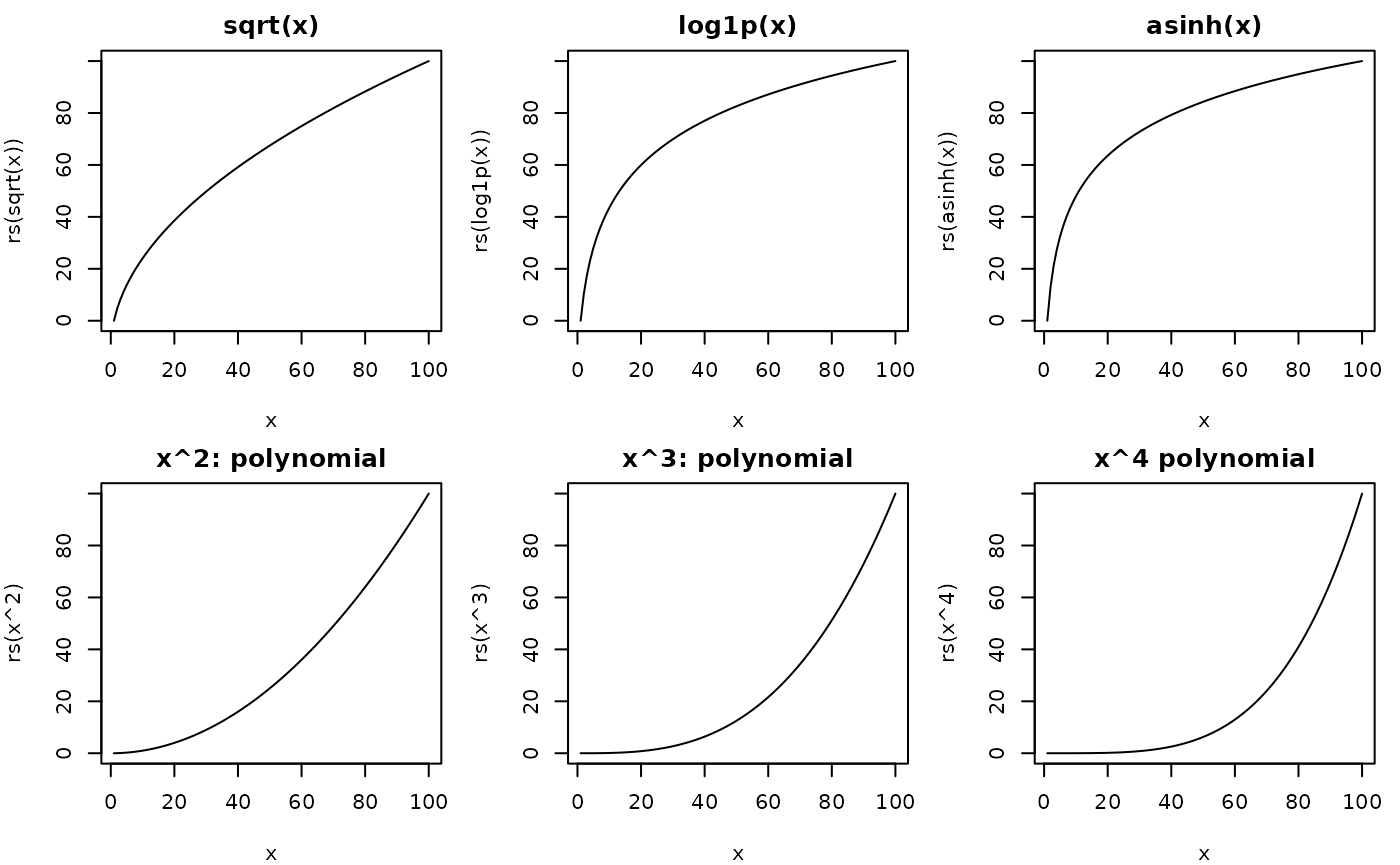
rm(x)We will apply a fourth order polynomial to the input tri data to accomodate a non-linear effect.
tri_rscl <- app(tri, function(x) { rs(x^2, to = c(1, 80)) })
par(mfrow = c(1, 2), mar = c(4, 4, 2, 1))
plot(tri, main = 'Original')
plot(tri_rscl, main = 'Rescaled')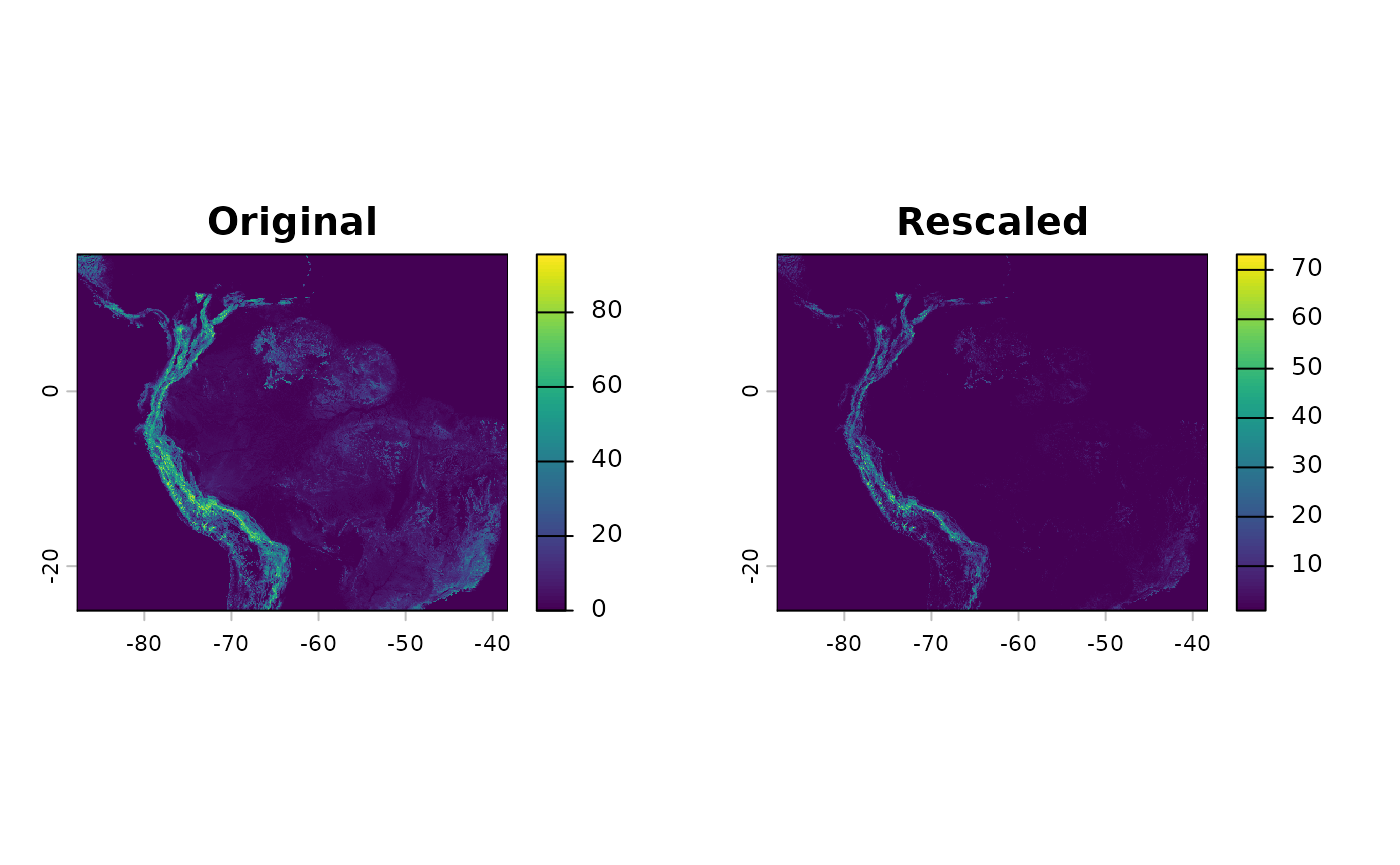
And we can create a new resistance surface
res_surface <- buildResistanceSurface(
base_raster = rast(ocean_r), # template
oceans = ocean_r, # rasters
lakes = lakes_r,
rivers = rivers_r,
#tri = tri, # dont use me! i rescale.
habitat = inverted_sdm,
addtl_r = tri_rscl,
w_ocean = 120, # weights to multiple input raster values by --
w_lakes = 70, # is 1 * 50
w_rivers = 40, # is 1 *20
w_habitat = 0.5,
#w_tri = 4 # don't use me! use addtl_wt
addtl_w = 1
)
dev.off()
#> null device
#> 1
plot(res_surface)